what would 1111111100 be converted to in hexadecimal?

Hex Reckoner

Hexadecimal Adding—Add together, Subtract, Multiply, or Divide

= ?

Convert Hexadecimal Value to Decimal Value

Hexadecimal Value: = ?

Convert Decimal Value to Hexadecimal Value

Decimal Value: = ?

The hexadecimal number system (hex) functions about identically to the decimal and binary systems. Instead of using a base of 10 or ii respectively, it uses a base of 16. Hex uses sixteen digits including 0-9, just equally the decimal system does, but also uses the letters A, B, C, D, Eastward, and F (equivalent to a, b, c, d, due east, f) to represent the numbers 10-fifteen. Every hex digit represents 4 binary digits, called nibbles, which makes representing large binary numbers simpler. For example, the binary value of 1010101010 can be represented equally 2AA in hex. This helps computers to compress large binary values in a manner that can exist easily converted between the two systems.

Below are some typical conversions between hex, binary, and decimal values:

Hex/Decimal Conversion

Hex	Binary	Decimal
0	0	0
1	1	1
two	ten	2
3	11	three
4	100	4
5	101	5
6	110	6
7	111	7
8	1000	8
9	1001	ix
A	1010	10
B	1011	eleven
C	1100	12
D	1101	thirteen
E	1110	14
F	1111	15
xiv	10100	20
3F	111111	63

Converting between decimal and hex involves understanding the identify values of the different number systems. A more in-depth discussion is bachelor on the binary calculator page. Note that converting between decimal and hex is quite similar to converting between decimal and binary. The ability to perform the conversion of either should brand the other relatively uncomplicated. As previously mentioned, hex functions using the base of 16. This means that for the value 2AA, each place value represents a power of xvi. Starting from the right, the first "A" represents the "ones" place, or 16⁰. The 2nd "A" from the right represents xviⁱ, and the 2 represents 16². Recall that "A" in hex is equivalent to 10 in decimal. Knowing this information, it is and then possible to convert from hex to decimal, as shown below:

EX:	2AA = (2 × xvi2) + (A × 161) + (A × 160)
	= (2 × 256) + (x × 16) + (ten × ane)
	= 512 + 160 + 10 = 682

Converting from decimal to hex is slightly more involved, simply uses the same concepts. Refer to the steps and examples beneath. It is important to work through the example provided in conjunction with the listed steps in order to understand the process:

1. Find the largest power of sixteen that is less than or equal to the number to exist converted, which volition exist referred to every bit X.
2. Make up one's mind how many times the power of xvi found in Step i goes into X, and take note of that number.
3. Multiply the number institute in Step 2 by the power of 16 and subtract this value from X. This new value will be referred to every bit Y.
   • Note that the number constitute in Step 2 volition exist the value written in the place value for the power of 16 that was plant. If, for example, the largest power of 16 was found to be 16⁴, and the number in Step ii was institute to exist iii, the hex value would accept the number 3 in its sixteen⁴ place value: 3qrst, where qrst represents the sixteen^{0 through 3} place values.
4. Echo Steps 1-3 using Y as the new starting value. Keep the procedure until 16 is larger than the remaining value, and assign the residuum to the xvi⁰ place value.
5. Assign each of the values constitute in each iteration of Step 2 to its respective place value to determine the hex value.

EX:	Convert decimal 1500 to hex
	(1)	Largest ability = 162 = 256
	(2)	256 × five = 1280, so (5 × sixteentwo)
	(iii)	1500 - 1280 = 220
	(4)	sixteen × xiii = 208, so (13 × sixteenone)
	(5)	220 - 208 = 12
	(6)	16 is larger than 12, so 12 is the value in the 160 place value
	(7)	1500 = (v × 16ii) + (13 × sixteenone) + (12 × 160)
	(8)	Remember that 10-15 take letter numerals In hex: 13 = D, and 12 = C
	(ix)	Therefore the hex value of 1500 is: 5DC

Converting from hex to decimal utilizes the aforementioned principles, but is arguably simpler. Multiply each digit in the hex value by its corresponding place value, and find the sum of each result. The process is the same regardless of whether the hex value contains letter numerals or non.

EX:	Convert hex 1024 to decimal
	(one)	(1 × sixteen3) + (0 × 16two) + (2 × 16one) + (iv × 160)
	(2)	4096 + 0 + 32 + 4 = 4132

Hex Addition

Hex addition follows the aforementioned rules as decimal addition with the only divergence being the added numerals A, B, C, D, Due east, and F. Information technology may exist user-friendly to have the decimal equivalent values of A through F handy when performing hex operations if the values have not yet been committed to memory. Below is an example of hex addition. Work through the example, and refer to the text below it for further details.

EX:

		1eight	1A	B
+		B	7	8
=	ane	4	ii	iii

Hex addition involves computing basic decimal improver while converting between hex and decimal when values larger than 9 (the numerals A through F) are nowadays. In the example above, B + 8 in decimal is eleven + viii = 19. 19_decimal is thirteen_hex, since there is 1 set of 16, with 3 left over. Just like in decimal addition, the 1 carries over to the next column. Hence, the next column works out to be 1 + A (10) + 7 = eighteen_decimal, or 12_hex. Conduct over the 1 to the final column resulting in 1 + 8 + B (11) = 20_decimal, or xiv_hex. This yields the outcome of 1423_hex.

Hex Subtraction

Hex subtraction can be computed much the same way as hex addition; by performing the operation while converting between hex and decimal values. The virtually significant departure between hex and decimal subtraction involves borrowing. When borrowing in hex, the "i" that is borrowed represents sixteen_decimal rather than x_decimal. This is because the column that is being borrowed from is sixteen times larger than the borrowing column (the aforementioned reason that the borrowed one in decimal represents x). As long every bit this is noted, and conversions of the letter of the alphabet numerals A-F are done carefully, hex subtraction is non any more than difficult than decimal subtraction. Work through the instance, and refer to the text below it for further details.

EX:

		5	D	1C
–		iii	A	F
=		two	2	D

In the first column on the right of the above example, C, or 12_decimal, is smaller than F, or xv_decimal. As such, it is necessary to borrow from the adjacent column. This reduces the D, to C, and lends 1, or 16_decimal to the outset column. 16_decimal + 12_decimal - xv_decimal = xiii_decimal, or D in the start column. The following columns require no borrowing, making the calculations simple. Since 1 was borrowed, C - A = 12_decimal - 10_decimal = ii, and 5 - iii = two yielding the terminal upshot of 22D. In the case where the number being subtracted is larger than the number existence subtracted from, merely change the positions of the numbers, calculate the subtraction, and add a negative sign to the result. If the above instance were instead 3AF - 5DC, it would then be written as is, except that the solution would exist -22D.

Hex Multiplication

Hex multiplication can be catchy because the conversions between hex and decimal when performing the operations require more effort since the numerals tend to exist larger. Having a hexadecimal multiplication table tin exist helpful (one is provided below). Otherwise, transmission conversion between decimal and hex will be necessary for each step. Beneath is an example of hex multiplication. To the correct of the example, each of the multiplication and addition steps is shown. Notation that all of the numerals used are hex. Refer to the addition section if necessary.

EX:

			F	A	iii × A = 1E; ane carried to F
×			C	3	3 × F = 2D, + 1 = 2E
		2	Eastward	Eastward	C × A = 78; 7 carried to F
+	B	B	8	0	C × F = B4, + vii = BB
=	B	Due east	half-dozen	E

Hex Division

Long division in hex is identical to long sectionalization in decimal, except that the multiplication and subtraction occur in hex. It is also possible to convert to decimal and perform long segmentation in decimal, and so convert back once consummate. For illustrative purposes, the division case volition be calculated entirely in hex. As with multiplication, having a hexadecimal multiplication tabular array (i is provided below) would exist convenient while conducting hex division. Beneath is an instance. Note that all numerals in the example are hex. Although no borrowing occurs in the example below, remember that borrowing in hex results in 16_decimal being borrowed, rather than 10_decimal. Refer to the hex subtraction section for further details.

Hexadecimal Multiplication Table

jeansusenter.blogspot.com

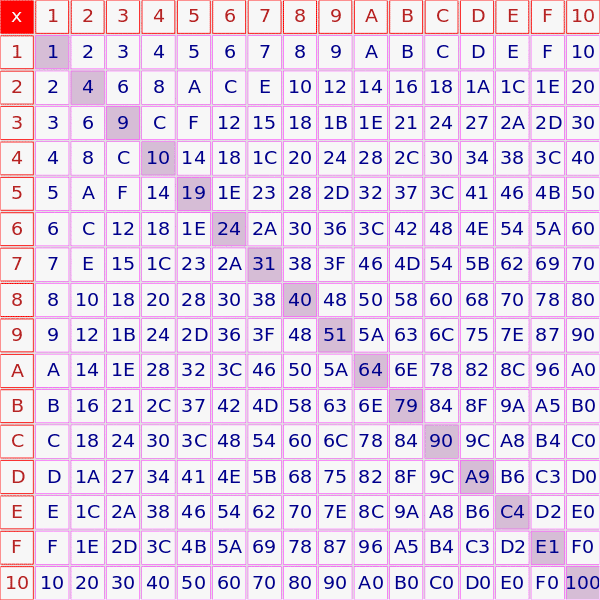
Source: https://www.calculator.net/hex-calculator.html

Share this post